Inside CG transformation (III).

最后看一下投影矩阵，这是最复杂的一个变换。我们只看透视投影矩阵，平行投影会简单很多。

在前面Cg Studying（http://leepyzh.blogspot.com/2009/09/cg-studying.html）一文中，我们已经看到了透视投影变换的过程：将平头视锥体变换了边长为2，中心在原点的立方体，以便于后面的裁剪和消隐工作。过程如下：

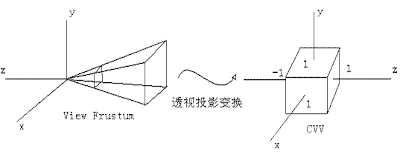下面将变换设定在常用的情况上，就是投影平面的中心和xy平面的中心重合，即在上面右图的Z轴上。OpenGL中构建投影矩阵的函数是gluPerspective，其原型是：

void gluPerspective(
　　GLdouble fovy, //角度
　　GLdouble aspect,//视景体的宽高比
　　GLdouble zNear,//沿z轴方向的两裁面之间的距离的近处
　　GLdouble zFar //沿z轴方向的两裁面之间的距离的远处
　　)

向x轴负方向看过去，这两个变换空间如下图所示。

考虑上边界情况，对于眼坐标系来说：y=-ztan(fovy/2), 而对于投影坐标系来说:y'=1.

很显然,y的映射为:y'=-y/(ztan(fovy/2)=-ycot(fovy/2)/z。 考虑z相同的情况，此时y‘是y的单调增函数（考虑y>0情况)。所以这个映射也符合视锥内部的点。

对于y的负边界来说，情况类似。对于x来说，只需额外除以aspect这个值即可，因为：

aspect = width/height = x宽度/y高度

所以：x' = -xcot(fovy/2)/z/aspect.

由于这是非线性变换，要解决除以z，可以借助齐次坐标w来进行。令w'=-z，于是：

x' = xcot(fovy/2)/aspect.

y' = ycot(fovy/2)

w'=-z

那么z呢？其实在屏幕上显示后，z值对于颜色没有任何贡献。但是，消隐少不了z值，也就是所谓的z缓冲。对于z变换来说，一定要保留两个点的z值大小顺序不变，另外，为了归一化处理，将其映射到[-1,1]之间。而最后我们还可以在OpenGL中用glDepthRange调节深度值，这一点说明从这里算出来的Z值到最终的深度值之间还会有一个映射调整。好，话说远了，回来看看z的变换。

那么所需的Z变换有以下约束：

1)z=-znear--->z'=-1;

2)z=-zfar---->z'=+1;

3)映射具有单调减性质（因为有负号，所以单调减）

4)最终z'还要除以w'=-z

根据以上条件，构造映射：

f(z) = -z*（Zfar+Znear） / ( Zfar – Znear ) – 2* Zfar*Znear / ( Zfar – Znear )

z'= f(z)/w' = （Zfar+Znear） / ( Zfar – Znear ) + [2* Zfar*Znear / ( Zfar – Znear )]/z

验证一下，上述几个条件都满足。你要是想正向推导这个公式，也是可以的。可以参考后面的文献。

还是直接给出代码，一看就清楚：

static const double myPi = 3.14159265358979323846;

static void buildPerspectiveMatrix(double fieldOfView,
double aspectRatio,
double zNear, double zFar,
float m[16])
{
double sine, cotangent, deltaZ;
double radians = fieldOfView / 2.0 * myPi / 180.0;

deltaZ = zFar - zNear;
sine = sin(radians);
/* Should be non-zero to avoid division by zero. */
assert(deltaZ);
assert(sine);
assert(aspectRatio);
cotangent = cos(radians) / sine;

m[0*4+0] = cotangent / aspectRatio;
m[0*4+1] = 0.0;
m[0*4+2] = 0.0;
m[0*4+3] = 0.0;

m[1*4+0] = 0.0;
m[1*4+1] = cotangent;
m[1*4+2] = 0.0;
m[1*4+3] = 0.0;

m[2*4+0] = 0.0;
m[2*4+1] = 0.0;
m[2*4+2] = -(zFar + zNear) / deltaZ;
m[2*4+3] = -2 * zNear * zFar / deltaZ;

m[3*4+0] = 0.0;
m[3*4+1] = 0.0;
m[3*4+2] = -1;
m[3*4+3] = 0;
}

至此，几个矩阵都推导完成了。

题外话：其实网上有很介绍矩阵的推导过程，包括很多教材上也有。但要真正理解，只有一种方法：实践出真知，自己动手。

Reference：
1. http://game.chinaitlab.com/arithmetic/28004.html；
2.http://blog.csdn.net/popy007/archive/2007/09/23/1797121.aspx；
3.http://blog.csdn.net/popy007/archive/2009/04/19/4091967.aspx。